- 为您提供最快捷、最准确、最权威、最丰富的田东教育信息
- 局内动态 | 学校动态 | 教育快报 | 通知公告 | 教育视频 |
- 教育概况 | 政策法规 | 办事指南 | 通知文件 | 行政许可 | 党建园地 | 工作制度 |
- 招生考试 | 组织人事 | 职成教育 | 基础教育 | 教育督导 | 教育工会 | 教学科研 | 捐资助学 | 信息化教育 |
- 教师风采 | 教学研究 | 教案荟萃 | 论文集锦 | 教育随笔 | 班级管理 | 师生作品 | 教育杂谈 |
- 明日之星 | 学生习作 | 箐箐校园 | 课堂内外 | 心理辅导 | 德育前沿 | 家长学校 | 健康之道 | 校园安全 | 留守儿童 |
- 活动剪影 | 得意之作 | 领导关怀 | 校园掠影 |
- 教育软件 | 教学课件 | 教案 | 试卷下载 | 课程资源 | 音频库 |
- 尚无数据
- 尚无数据
- 视频新闻|教学实况|文艺演出
激发内趋 促进思维发展
——数学思维教学的点滴体会
“数学是思维的体操”。当学生处于“心求通未得”,“口欲言未能”的思维受阻的临界状态时,教师要善于采用灵活有效的教学手段,创设情境,激发学生的兴趣,使学生的思维进入由不平衡到平衡,即“探究——深思——发现——解决问题”的思维活跃状态。把握学生思维活动的量和质,启发学生思维,促进积极思考是关键。如果学生思维尚未进入临界状态,教师则不急于介绍或讲解知识,而进一步启动学生的思维。如果学生在教师启发下,经过自己的思考,完成思维的全过程,得出正确的结论那么教者就不必讲授。这样既促进了学生思维的发展,又提高了学习效率。但在实际教学中往往有重教路轻学路,把握不住学生思维活动的发展趋势。
如何才能激发学生的内趋动力,让学生突破思维的临界点,在豁然开朗的愉悦情绪中,实现思维从量变到质变的飞跃,完成学习任务?教学中需要充分发掘学生内在潜力,促进其思维发展。
一、引导学生积极感知尝试,因势利导,深化思维,强化共生效应。
心理学的研究成果表明,感知是认知的基础,人通过视觉获取的信息约占大脑获取信息的85%。为此在数学教学中,应根据小学生好奇好动,学习兴趣易于激发的心理特点,充分发扬图解、演示、制作、电化教学直观形象之长,增强刺激强度,刺激视觉神经,引起学生的有意后注意。
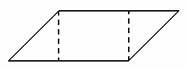
如在教平行四边形面积计算时,叫学生拿出事先准备好的等底等高的长方形和平行四边形硬纸片各一个,让学生动手度量,说出长方形的长与平行四边形的底、长方形的宽与平行四边形的高分别相等后,引其思考二者面积有什么关系?在学生进入积极思考并讨论后,教师再引其将两块硬纸板沿底叠加,引导观察,从而发现平行四边形上剪下多余的一部位补到另一部位,拼成长方形,然后然后操作,结果如下图: 在此原型启发下,因势利导:这个长方形是如何得到的,它与平行四边形有什么关系?(长方形的长就是平行四边形的底,长方形的宽就是平行四边形的高。)长方形的面积公式是什么?平行四边形面积怎样求?为什么?
让学生在看、做、思的过程中感知、领悟平行四边形的面积与它的底和高有关。这样由已知引出生长点,为学习未知作好铺垫,化难为易,使平行四边形面积计算这一重点在形象直观、轻松愉悦的氛围中突破,也为学习三角形、梯形及其它图形的面积打下良好的基础。 再如:在教完长方形和正方形的周长、面积计算后,教者用投影仪一步一步打出系列图形,让学生思考:下图中长方形发生了什么变化?(把一个长方形分成两个,再分成三个长方形。)变化后的图形总面积与总周长都发生了变化吗?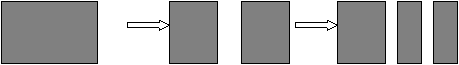 厘
米
5厘米
练习后,再让学生撕纸条,再说一说纸张总面积与总周长的变与不变。这样就让学生在系列渐变的图形中,理解到一个图形分成若干个图形,它的总面积不变,而总周长增加,因为分割后总会多出若干条边。从而加深对面积与周长概念的理解,正确区分这两个基本概念的不同点。这样通过观察、操作、思考、表述、讨论激发学生学习的内趋动力,协同多种器官参与活动使数学是研究现实世界“空间形式”和“数量关系”的思想逐步在学生头脑中建立,提高思维品质,培养合作精神。
二、激发学生分析思考,适时引导,优化激活效应
根据学生思维活动的发展趋势,创设发现问题的情境,激起思维冲动、促其展开思维的双翅,逐步将学生的思维激活。
例如:在教这样一道题目时“客车以每小时40千米的速度从甲地开往乙地,行半小时后,一辆货车以每小时35千米的速度从乙地开往甲地,客车开出4.5小时时两车相遇,甲乙两地相距多远?适时启发:1、要求甲乙两地的距离,必须知道哪些条件?2、客车、货车各行驶多少时间?为什么?
学生列出算式40Х0.5+(40+35)Х(45-0.5)后,引导其思考不同解法,接着将题改成一客车开出前40分钟,货车从乙地开出,问学生又怎样解?还可以怎样解?哪一种方法更简便?
再让其根据下式编一道行程应用题:
5083÷4+(50+40)Х5
进而引导学生思考解此类题的规律。即先行的路程+两车同时行的路程=甲乙两地的距离,或客车行的千米数+货车行的千米=甲乙两地的距离。
这样通过分析思考、灵活多变,深入探求,激活学生思维,以疑、奇、趣促其思考,激其创造,唤醒其潜能,使数学教学真正成为“数学活动(思维活动)的教学”。使激活效应得以优化。
三、使学生理解领悟,择机引导,催化升腾效应。
设疑、激疑往往能激起学生思维的撞击,激起智慧的火花,更能加深理解,促进领悟。
在教学三角形内角之和等于180度的知识后,择机导“操”,设疑,将一个三角形分成两个三角形之后,其内角和等于多少?将等高的两个直角三角形,沿高拼成一个三角形后,内角和又为多少?为什么?学生通过思考理解到:前者将一个角分解成两个角,且增加了两个和为180度的角;后者将两个合并为一个角,且刚好减少了两个和为180度的直角。同时以多媒体或实物演示促其顿悟,并认识到事物是发展变化的,具体情况要作具体分析。
在教学工程问题后,出了这样一道选择题:某工程队要修一条长2400米的公路,第一小队独修30天完成,第二小队独修20天完成,两队合修多少天完成?
A.正确列式为( );
B.计算简便的列式为( );
C.列式错误的为( )。
1. 2400÷(2400÷30+2400÷20)
2. 1÷(1÷30+1÷20)
3. 2400÷(1÷30+1÷20)
为什么?让学生体会到数学上殊途同归的神奇,从而教育学生要善于随机应变,选择最佳的解题思路。这其实就是围绕选择题巧设陷阱,有意让学生暴露解题障碍,又在其选择的过程中促其争相发言,争述其理。工作总量与工作效率之间的对应关系在质疑、释疑的氛围中进一步明确,触及知识本质,催化认知升腾。
厘
米
5厘米
练习后,再让学生撕纸条,再说一说纸张总面积与总周长的变与不变。这样就让学生在系列渐变的图形中,理解到一个图形分成若干个图形,它的总面积不变,而总周长增加,因为分割后总会多出若干条边。从而加深对面积与周长概念的理解,正确区分这两个基本概念的不同点。这样通过观察、操作、思考、表述、讨论激发学生学习的内趋动力,协同多种器官参与活动使数学是研究现实世界“空间形式”和“数量关系”的思想逐步在学生头脑中建立,提高思维品质,培养合作精神。
二、激发学生分析思考,适时引导,优化激活效应
根据学生思维活动的发展趋势,创设发现问题的情境,激起思维冲动、促其展开思维的双翅,逐步将学生的思维激活。
例如:在教这样一道题目时“客车以每小时40千米的速度从甲地开往乙地,行半小时后,一辆货车以每小时35千米的速度从乙地开往甲地,客车开出4.5小时时两车相遇,甲乙两地相距多远?适时启发:1、要求甲乙两地的距离,必须知道哪些条件?2、客车、货车各行驶多少时间?为什么?
学生列出算式40Х0.5+(40+35)Х(45-0.5)后,引导其思考不同解法,接着将题改成一客车开出前40分钟,货车从乙地开出,问学生又怎样解?还可以怎样解?哪一种方法更简便?
再让其根据下式编一道行程应用题:
5083÷4+(50+40)Х5
进而引导学生思考解此类题的规律。即先行的路程+两车同时行的路程=甲乙两地的距离,或客车行的千米数+货车行的千米=甲乙两地的距离。
这样通过分析思考、灵活多变,深入探求,激活学生思维,以疑、奇、趣促其思考,激其创造,唤醒其潜能,使数学教学真正成为“数学活动(思维活动)的教学”。使激活效应得以优化。
三、使学生理解领悟,择机引导,催化升腾效应。
设疑、激疑往往能激起学生思维的撞击,激起智慧的火花,更能加深理解,促进领悟。
在教学三角形内角之和等于180度的知识后,择机导“操”,设疑,将一个三角形分成两个三角形之后,其内角和等于多少?将等高的两个直角三角形,沿高拼成一个三角形后,内角和又为多少?为什么?学生通过思考理解到:前者将一个角分解成两个角,且增加了两个和为180度的角;后者将两个合并为一个角,且刚好减少了两个和为180度的直角。同时以多媒体或实物演示促其顿悟,并认识到事物是发展变化的,具体情况要作具体分析。
在教学工程问题后,出了这样一道选择题:某工程队要修一条长2400米的公路,第一小队独修30天完成,第二小队独修20天完成,两队合修多少天完成?
A.正确列式为( );
B.计算简便的列式为( );
C.列式错误的为( )。
1. 2400÷(2400÷30+2400÷20)
2. 1÷(1÷30+1÷20)
3. 2400÷(1÷30+1÷20)
为什么?让学生体会到数学上殊途同归的神奇,从而教育学生要善于随机应变,选择最佳的解题思路。这其实就是围绕选择题巧设陷阱,有意让学生暴露解题障碍,又在其选择的过程中促其争相发言,争述其理。工作总量与工作效率之间的对应关系在质疑、释疑的氛围中进一步明确,触及知识本质,催化认知升腾。
如在教平行四边形面积计算时,叫学生拿出事先准备好的等底等高的长方形和平行四边形硬纸片各一个,让学生动手度量,说出长方形的长与平行四边形的底、长方形的宽与平行四边形的高分别相等后,引其思考二者面积有什么关系?在学生进入积极思考并讨论后,教师再引其将两块硬纸板沿底叠加,引导观察,从而发现平行四边形上剪下多余的一部位补到另一部位,拼成长方形,然后然后操作,结果如下图: 在此原型启发下,因势利导:这个长方形是如何得到的,它与平行四边形有什么关系?(长方形的长就是平行四边形的底,长方形的宽就是平行四边形的高。)长方形的面积公式是什么?平行四边形面积怎样求?为什么?
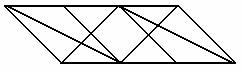
又如在教完同底等高的平行四边形相等后,出示下图。并提问:下图中哪些图形面积相等?为什么?
让学生在看、做、思的过程中感知、领悟平行四边形的面积与它的底和高有关。这样由已知引出生长点,为学习未知作好铺垫,化难为易,使平行四边形面积计算这一重点在形象直观、轻松愉悦的氛围中突破,也为学习三角形、梯形及其它图形的面积打下良好的基础。 再如:在教完长方形和正方形的周长、面积计算后,教者用投影仪一步一步打出系列图形,让学生思考:下图中长方形发生了什么变化?(把一个长方形分成两个,再分成三个长方形。)变化后的图形总面积与总周长都发生了变化吗?
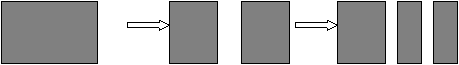 厘
米
5厘米
练习后,再让学生撕纸条,再说一说纸张总面积与总周长的变与不变。这样就让学生在系列渐变的图形中,理解到一个图形分成若干个图形,它的总面积不变,而总周长增加,因为分割后总会多出若干条边。从而加深对面积与周长概念的理解,正确区分这两个基本概念的不同点。这样通过观察、操作、思考、表述、讨论激发学生学习的内趋动力,协同多种器官参与活动使数学是研究现实世界“空间形式”和“数量关系”的思想逐步在学生头脑中建立,提高思维品质,培养合作精神。
二、激发学生分析思考,适时引导,优化激活效应
根据学生思维活动的发展趋势,创设发现问题的情境,激起思维冲动、促其展开思维的双翅,逐步将学生的思维激活。
例如:在教这样一道题目时“客车以每小时40千米的速度从甲地开往乙地,行半小时后,一辆货车以每小时35千米的速度从乙地开往甲地,客车开出4.5小时时两车相遇,甲乙两地相距多远?适时启发:1、要求甲乙两地的距离,必须知道哪些条件?2、客车、货车各行驶多少时间?为什么?
学生列出算式40Х0.5+(40+35)Х(45-0.5)后,引导其思考不同解法,接着将题改成一客车开出前40分钟,货车从乙地开出,问学生又怎样解?还可以怎样解?哪一种方法更简便?
再让其根据下式编一道行程应用题:
5083÷4+(50+40)Х5
进而引导学生思考解此类题的规律。即先行的路程+两车同时行的路程=甲乙两地的距离,或客车行的千米数+货车行的千米=甲乙两地的距离。
这样通过分析思考、灵活多变,深入探求,激活学生思维,以疑、奇、趣促其思考,激其创造,唤醒其潜能,使数学教学真正成为“数学活动(思维活动)的教学”。使激活效应得以优化。
三、使学生理解领悟,择机引导,催化升腾效应。
设疑、激疑往往能激起学生思维的撞击,激起智慧的火花,更能加深理解,促进领悟。
在教学三角形内角之和等于180度的知识后,择机导“操”,设疑,将一个三角形分成两个三角形之后,其内角和等于多少?将等高的两个直角三角形,沿高拼成一个三角形后,内角和又为多少?为什么?学生通过思考理解到:前者将一个角分解成两个角,且增加了两个和为180度的角;后者将两个合并为一个角,且刚好减少了两个和为180度的直角。同时以多媒体或实物演示促其顿悟,并认识到事物是发展变化的,具体情况要作具体分析。
在教学工程问题后,出了这样一道选择题:某工程队要修一条长2400米的公路,第一小队独修30天完成,第二小队独修20天完成,两队合修多少天完成?
A.正确列式为( );
B.计算简便的列式为( );
C.列式错误的为( )。
1. 2400÷(2400÷30+2400÷20)
2. 1÷(1÷30+1÷20)
3. 2400÷(1÷30+1÷20)
为什么?让学生体会到数学上殊途同归的神奇,从而教育学生要善于随机应变,选择最佳的解题思路。这其实就是围绕选择题巧设陷阱,有意让学生暴露解题障碍,又在其选择的过程中促其争相发言,争述其理。工作总量与工作效率之间的对应关系在质疑、释疑的氛围中进一步明确,触及知识本质,催化认知升腾。
厘
米
5厘米
练习后,再让学生撕纸条,再说一说纸张总面积与总周长的变与不变。这样就让学生在系列渐变的图形中,理解到一个图形分成若干个图形,它的总面积不变,而总周长增加,因为分割后总会多出若干条边。从而加深对面积与周长概念的理解,正确区分这两个基本概念的不同点。这样通过观察、操作、思考、表述、讨论激发学生学习的内趋动力,协同多种器官参与活动使数学是研究现实世界“空间形式”和“数量关系”的思想逐步在学生头脑中建立,提高思维品质,培养合作精神。
二、激发学生分析思考,适时引导,优化激活效应
根据学生思维活动的发展趋势,创设发现问题的情境,激起思维冲动、促其展开思维的双翅,逐步将学生的思维激活。
例如:在教这样一道题目时“客车以每小时40千米的速度从甲地开往乙地,行半小时后,一辆货车以每小时35千米的速度从乙地开往甲地,客车开出4.5小时时两车相遇,甲乙两地相距多远?适时启发:1、要求甲乙两地的距离,必须知道哪些条件?2、客车、货车各行驶多少时间?为什么?
学生列出算式40Х0.5+(40+35)Х(45-0.5)后,引导其思考不同解法,接着将题改成一客车开出前40分钟,货车从乙地开出,问学生又怎样解?还可以怎样解?哪一种方法更简便?
再让其根据下式编一道行程应用题:
5083÷4+(50+40)Х5
进而引导学生思考解此类题的规律。即先行的路程+两车同时行的路程=甲乙两地的距离,或客车行的千米数+货车行的千米=甲乙两地的距离。
这样通过分析思考、灵活多变,深入探求,激活学生思维,以疑、奇、趣促其思考,激其创造,唤醒其潜能,使数学教学真正成为“数学活动(思维活动)的教学”。使激活效应得以优化。
三、使学生理解领悟,择机引导,催化升腾效应。
设疑、激疑往往能激起学生思维的撞击,激起智慧的火花,更能加深理解,促进领悟。
在教学三角形内角之和等于180度的知识后,择机导“操”,设疑,将一个三角形分成两个三角形之后,其内角和等于多少?将等高的两个直角三角形,沿高拼成一个三角形后,内角和又为多少?为什么?学生通过思考理解到:前者将一个角分解成两个角,且增加了两个和为180度的角;后者将两个合并为一个角,且刚好减少了两个和为180度的直角。同时以多媒体或实物演示促其顿悟,并认识到事物是发展变化的,具体情况要作具体分析。
在教学工程问题后,出了这样一道选择题:某工程队要修一条长2400米的公路,第一小队独修30天完成,第二小队独修20天完成,两队合修多少天完成?
A.正确列式为( );
B.计算简便的列式为( );
C.列式错误的为( )。
1. 2400÷(2400÷30+2400÷20)
2. 1÷(1÷30+1÷20)
3. 2400÷(1÷30+1÷20)
为什么?让学生体会到数学上殊途同归的神奇,从而教育学生要善于随机应变,选择最佳的解题思路。这其实就是围绕选择题巧设陷阱,有意让学生暴露解题障碍,又在其选择的过程中促其争相发言,争述其理。工作总量与工作效率之间的对应关系在质疑、释疑的氛围中进一步明确,触及知识本质,催化认知升腾。
文章录入:周周 责任编辑:周美娟
 网友评论:(评论内容只代表网友观点,与本站立场无关!)
网友评论:(评论内容只代表网友观点,与本站立场无关!)
数据载入中,请稍后……

>> 专题栏目